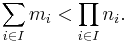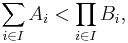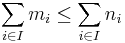König's theorem (set theory)

In set theory, König's theorem (named after the Hungarian mathematician Gyula Kőnig, who published under the name Julius König) colloquially states that if the Axiom of Choice holds, I is a set, m_i and n_i are cardinal numbers for every i in I, and 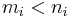$m_i < n_i \!$ for every i in I then

$\sum_{i\in I}m_i<\prod_{i\in I}n_i.$

The sum here is the cardinality of the disjoint union of the sets m_i and the product is the cardinality of the cartesian product. However, without the use of the Axiom of Choice, the sum and the product cannot be defined as cardinal numbers, and the meaning of the inequality sign would need to be clarified.

1 Details
2 Corollaries of König's theorem
- 2.1 Axiom of choice
- 2.2 König's theorem and cofinality
3 A proof of König's theorem
4 Notes
5 References
6 External links

Details

The precise statement of the result: if I is a set , A_i and B_i are sets for every i in I, and 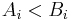$A_i<B_i\!$ for every i in I then

$\sum_{i\in I}A_i<\prod_{i\in I}B_i,$

where < means strictly less than in cardinality, i.e. there is an injective function from A_i to B_i, but not one going the other way. The union involved need not be disjoint (a non-disjoint union can't be any bigger than the disjoint version, also assuming the axiom of choice). In this formulation, König's theorem is equivalent to the Axiom of Choice.^[1]

(Of course, König's theorem is trivial if the cardinal numbers m_i and n_i are finite and the index set I is finite. If I is empty, then the left sum is the empty sum and therefore 0, while the right hand product is the empty product and therefore 1).

König's theorem is remarkable because of the strict inequality in the conclusion. There are many easy rules for the arithmetic of infinite sums and products of cardinals in which one can only conclude a weak inequality ≤, for example: IF 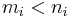$m_i < n_i \!$ for all i in I, THEN one can only conclude

$\sum_{i\in I} m_i \le \sum_{i\in I} n_i$

since, for example, setting 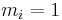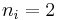$m_i = 1$ & $n_i = 2$ where the index set I is the natural numbers, yields the sum 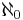$\aleph_0$ for both sides and we have a strict equality.

Corollaries of König's theorem

If 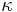$\kappa\,$ is a cardinal then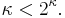 $\kappa < 2^{\kappa}.\!$

If we take m_i = 1, and n_i = 2 for each i in κ, then the left hand side of the above inequality is just κ, while the right hand side is 2^κ, the cardinality of functions from κ to {0,1}, that is, the cardinality of the power set of κ. Thus, König's theorem gives us an alternate proof of Cantor's theorem. (Historically of course Cantor's theorem was proved much earlier.)

Axiom of choice

One way of stating the axiom of choice is "An arbitrary Cartesian product of non-empty sets is non-empty.". Let B_i be a non-empty set for each i in I. Let A_i = {} for each i in I. Thus by König's theorem, we have:

If 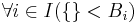$\forall i\in I(\{\}<B_i)$ , then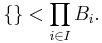 $\{\}<\prod_{i\in I}B_i.$

That is, the Cartesian product of the given non-empty sets, B_i, has a larger cardinality than the sum of empty sets. Thus it is non-empty which is just what the axiom of choice states. Since the axiom of choice follows from König's theorem, we will use the axiom of choice freely and implicitly when discussing consequences of the theorem.

König's theorem and cofinality

König's theorem has also important consequences for cofinality of cardinal numbers.

If 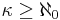$\kappa\ge\aleph_0$ , then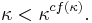 $\kappa<\kappa^{cf(\kappa)}. \!$

Choose a strictly increasing cf(κ)-sequence of cardinals approaching κ. Each of them is less than κ, so their sum which is κ is less than the product of cf(κ) copies of κ.

According to Easton's theorem, the next consequence of König's theorem is the only nontrivial constraint on the continuum function for regular cardinals.

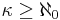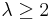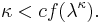
If $\kappa\geq\aleph_0$ and $\lambda\geq 2$ , then $\kappa<cf(\lambda^\kappa).\!$

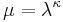Let $\mu = \lambda^\kappa \!$ . Suppose that, contrary to this corollary, 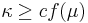$\kappa \ge cf(\mu)$ . Then using the previous corollary, 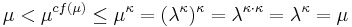$\mu<\mu^{cf(\mu)}\le\mu^{\kappa}=(\lambda^\kappa)^\kappa=\lambda^{\kappa\cdot\kappa}=\lambda^\kappa=\mu$ , a contradiction. Thus the supposition must be false and this corollary must be true.

A proof of König's theorem

Assuming Zermelo–Fraenkel set theory, including especially the axiom of choice, we can prove the theorem. Remember that we are given 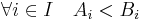$\forall i\in I\quad A_i<B_i$ , and we want to show :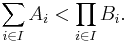 $\sum_{i\in I}A_i<\prod_{i\in I}B_i.$

First, we show that there is an injection from the sum to the product. Using the axiom of choice, for each i we choose an injection f_i from A_i to B_i. Notice that f_i cannot be a surjection because then its inverse would be an injection from B_i to A_i. So, for each i, there must be an element of B_i not in the range of f_i. Using the axiom of choice again, we choose such an x_i for each i. Define g on the sum by g(i,a) (j) = f_i(a) when j = i and a is an element of A_i and g(i,a) (j) = x_j when j ≠ i and a is an element of A_i. Since f_i(a) ≠ x_i for each i, g is an injection from the sum to the product.

Second, we show that there is no injection h from the product to the sum. Suppose, to the contrary, that such an h existed. In a similar manner to Cantor's diagonal argument, we will construct an element e of the product, which cannot have a value under h. For each i in I, construct a partial function f_i from A_i to B_i by f_i(a) = d(i) if there is a d in the product such that h(d) = (i,a). (This is a partial function because h is an injection, so the d is unique.) If f_i were a surjection, then, using the axiom of choice, we could construct an injection g from B_i into A_i (g would be a right inverse of f_i), contradicting the hypothesis. Hence, for each i in I, there are elements of B_i not in the image of f_i. So using the axiom of choice again, we choose e(i) in B_i but not in the image of f_i. Consider, now, the value of h(e) = (i,c) with c in A_i. But then f_i(c) = e(i), contradicting the construction of e. Hence no such injection can exist, and the product is strictly larger in cardinality than the sum.

Notes

^ Rubin, H.; Rubin, J.E. (1985). Equivalents of the Axiom of Choice, II. New York, NY: North Holland. pp. 185. ISBN 0-444-87708-8.

References

M. Holz, K. Steffens and E. Weitz (1999). Introduction to Cardinal Arithmetic. Birkhäuser. ISBN 3764361247.

External links

König's theorem article on PlanetMath, includes a proof